SITE OPTIMISÉ POUR EDGE, MOZILLA FIREFOX et CHROME
AFFICHAGE 1920 X 1080
SITE OPTIMISÉ POUR EDGE, MOZILLA FIREFOX et CHROME
AFFICHAGE 1920 X 1080
SITE OPTIMISÉ POUR EDGE, MOZILLA FIREFOX et CHROME
AFFICHAGE 1920 X 1080
La page
La page
La page
mineralogie.club
19 Mai : Nouvelle page "Cumengéite et Boléite"
14 Juin : La dernière version téléchargeable de la Charte Internationale Chronostratigraphique en français
14 Juin : Mise à jour des Photos de la semaine
CRISTALLOGRAPHIE
Page I Généralités
"La cristallographie démontre les propriétés générales de l'état cristallin."
SOMMAIRE DE LA PAGE
DÉFINITIONS
PRINCIPES
NOTATION DE MILLER
ÉLÉMENTS DE SYMÉTRIE
APPROFONDIR, RÉSUMER, CONCLURE
GLOSSAIRE DE LA PAGE
BIBLIOGRAPHIE
VIDEO
Cliquez
ORIGINE DE LA CRISTALLOGRAPHIE
A l’origine la cristallographie était une branche de la minéralogie purement descriptive car on ignorait qu’elle pouvait avoir d’autres domaines d’applications.
La cristallographie est la science de l’étude, à l’échelle atomique, des matières cristallines dont les caractères et propriétés physico-chimiques sont liés à la disposition spatiale des atomes, qui les composent.
L’unité de base du cristal est la « maille élémentaire » qui est transposées dans les trois dimensions.
Cristal est un mot d’origine grecque, « Krustallas », qui signifiait « solidifié par le froid ». A cette époque antique on imaginait que le cristal de roche, le quartz, était la transformation de la glace par le froid.
DEFINITION
Une matière cristalline est un matériau à l'état solide dont les composants chimiques, atomes et molécules sont disposés selon un schéma ordonné tridimensionnel.
En théorie les faces d'un cristal sont des surfaces planes. Dans la nature les minéraux se forment dans des conditions qui ne permettent pas toujours un développement parfait, ils sont souvent gênés dans leur croissance, ils sont xénomorphes. Lorsqu'un solide n'est pas cristallin on dit qu'il est amorphe (sans forme).
Dans un matériau amorphe les caractéristiques physiques et chimiques sont identiques dans toutes les directions. Dans un cristal elles varient selon les directions.
" Le cristal c'est la nature ordonnée. "
Quelques exemple de cristaux découlant du cube.
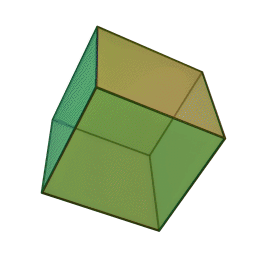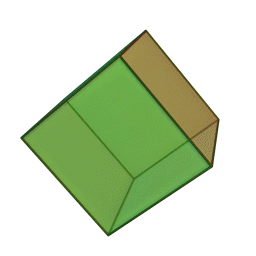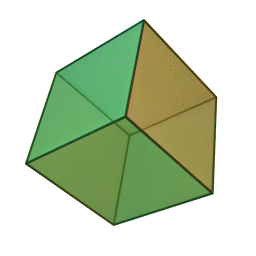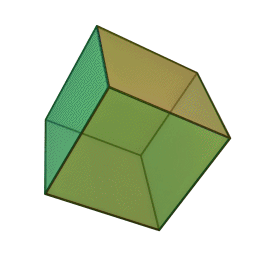
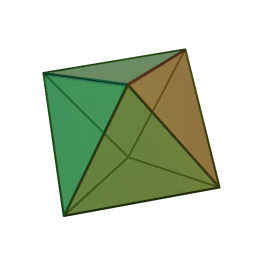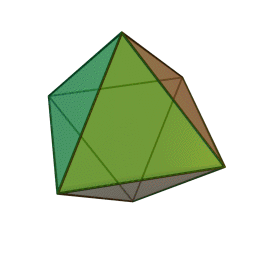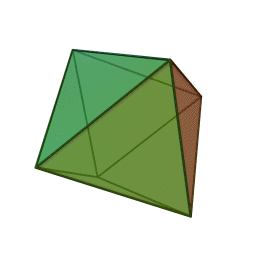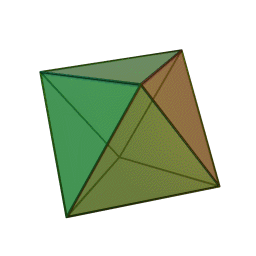
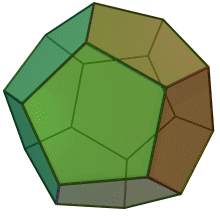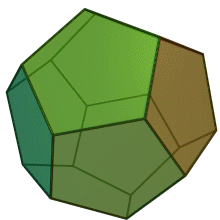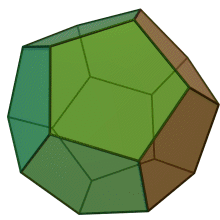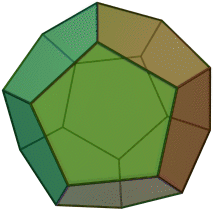
Cube
Octaèdre
Tétraèdre
Dodécaèdre
Dodécaèdre rhombique
PRINCIPES
Principe N°1
Dans une espèce minérale la valeur des angles dièdres est constante même si la forme varie.
Le goniomètre est utilisé pour mesurer les angles des cristaux.
Troncature
Principe N°2
Les cristaux ont une structure "périodique" en réseau. Un rhomboèdre de 5 centimètres est formé de milliers de rhomboèdres identiques. Le plus petit volume formant un cristal est appelé maille élémentaire que l'on peut assimiler à un parallélépipède quelconque que l'on défini par la longueur de trois arêtes adjacentes ou axes cristallographiques.
Principe N°3
Les diverses formes cristallines que peut prendre une espèce minérale découlent toutes du parallélépipède homothétique de la maille élémentaire par un phénomène de troncature où une surface va remplacer soit un sommet, soit une arête.
NOTATION DE MILLER
La notation de Miller permet de nommer les faces d'un cristal, dans un système à trois dimensions.
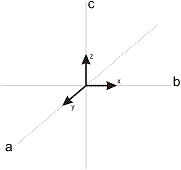
Il y a différentes possibilités pour qu’un plan (qui représente une face d’un cristal) coupe les axes tridimensionnels.
Ce plan peut couper 1, 2 ou 3 axes, a, b et c, on note 1 quand l'axe est coupé, on note 0 quand le plan est parallèle a un axe exemple :
Sur le schéma 1 il coupe l’axe B tout en étant parallèle aux axes A et C, on le note 010.
Sur le schéma 2 il coupe les axes B et C tout en étant parallèle à l’axe A on le note 011.
Sur le schéma 3 il coupe les trois axes A, B et C formant un angle équilatéral on le note 111.
On peut ainsi voir toutes les combinaisons :
Le plan coupe A seul en étant parallèle à B et C on note 100.
Le plan coupe B seul en étant parallèle à A et C on note 010.
Le plan coupe C seul en étant parallèle à A et B on note 001.
Le plan coupe A et B en étant parallèle à C on note 110.
Le Plan coupe A et C en étant parallèle à B on note 101.
Le plan coupe C et B en étant parallèle à A on note 011.
Comme on la vu sur le troisième dessin si le plan coupe les trois axes A, B et C en formant un triangle on note 111.
Lorsque les plans sont coupés dans la partie négative d’un axe on note ī (lire moins un)
LES ÉLÉMENTS DE SYMÉTRIE
Les principaux éléments de symétrie sont :
-
Le centre de symétrie
-
Les plans de symétrie
-
Les axes de symétrie
Centre de symétrie :
-
Point imaginaire où se croisent des lignes imaginaires joignant les sommets deux à deux. Ce centre est toujours noté C.
Plan de symétrie :
-
un plan de symétrie divise le cristal en deux moitiés qui sont le miroir l'une de l'autre.
Axe de symétrie :
-
Un axe de symétrie est un axe autour duquel on fait pivoter un cristal . Lors d'un rotation de 360°, si ce cristal se trouve dans une position qui semble identique à quatre reprise (à chaque quart de tour) l'axe de symétrie est dit d'ordre 4, s'il se retrouve dans une position identique 6 fois (rotations de 60°) on dira qu'il est d'ordre 6 :
-
ordre 2 rotations de 180°
-
ordre 3 rotations de 120°
-
ordre 4 rotations de 90°
-
ordre 6 rotations de 60°
-
Dans le cube sur la figure du haut nous avons représenté 3 axes de symétrie d'ordre 4.
Il manque les 6 axes d'ordre 2 et les 4 axes d'ordre 3.
Dans le cristal hexagonal, figure du bas, nous avons représenté tous les axes de symétrie, 1 d'ordre 6 et 3 d'ordre 2.
Axe inverse :
-
Un axe inverse est un axe autour du quel, lors de la rotation, le cristal se trouve dans une position identique inversée.
Glossaire de la page :
Homothétique
1 adjectif qualifiant un format proportionnel à un autre, en réduction ou agrandissement.
2 Se dit de formats dont les rapports latéraux sont égaux.
Xénomorphe
adj. du grec xenos : étranger et morphê : forme (anglais : xénomorphic), s'applique à un minéral qui, bien que cristallisé, présente une forme quelconque, les faces caractéristiques du système cristallin n'ayant pu se développer. Cela est dû généralement au fait que les les cristaux voisins, ou les éléments figurés voisins, déjà formés ont empêché ce développement.
Antonyme : automorphe
Synonyme allomorphe
Bibliographie :
La gemmologie, notions, principes, concepts, F. Fayette
Encyclopédie des minéraux, O. Johnsen
Les minéraux, E. Asselborn, H. Chaumeton, PJ. Chiappero, J. Galvier
Dictionnaire de géologie, A. Foucault, J.F. Raoult